Evaluating your championship order predictions (a mathsy post)

I see many content creators predict the order of the championship before the season (or even race results before each weekend). Then, I see them at the end of the season, attempting to evaluate their predictions. They usually go over the entire list, having emotional reactions to their picks - which, I admit, makes great content. However, for me, this approach is missing the overall verdict: How well did you predict the order?

Final Top 10 of the 2024 season - source: @F1 on X (Sorry if it doesn't show up on desktop. This picture is literally only here so that the post would have a thumbnail. You're not missing much.)

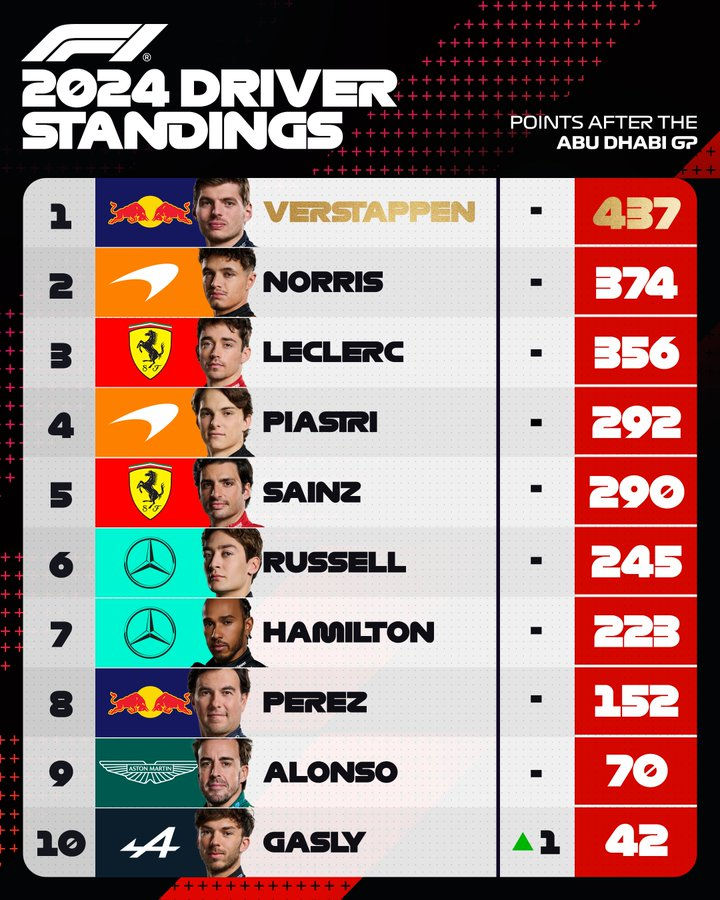
In this post, I am going to show you how to do a proper evaluation of your prediction, which yields a numerical value that you can use as some sort of score (which also allows you to compare your prediction to that of others). Fair warning: it is a bit mathsy/computer science-y, but I am going to keep it as simple and understandable as possible. Then, I will say a bit about the theoretical background because it is very close to one of my PhD theses, and I absolutely love the topic, but you can skip it if you like. Finally, I'll list some other variations of this method you may try.

Also, before we start, I should probably point out that even though this post is about Formula 1, what I am about to show you can obviously be applied to any other sport or any ranking. It doesn't even have to be a prediction. Just two different rankings of the same things. However, because this blog is about Formula 1, I will be showing this in the context of the pinnacle of motorsports.

The method

I will be using the constructors' championship as an example. Let's say that at the beginning of this season, I attempted to predict the final WCC order. I went conservative with my prediction, and I predicted last year's championship order (with some team name changes, obviously).

	Prediction/2023 WCC order	2024 WCC order
1.	Red Bull	McLaren
2.	Mercedes	Ferrari
3.	Ferrari	Red Bull
4.	McLaren	Mercedes
5.	Aston Martin	Aston Martin
6.	Alpine	Alpine
7.	Williams	Haas
8.	RB	RB
9.	Sauber	Williams
10.	Haas	Sauber

Naturally, the real order turned out different from my prediction, but how far off was I?

In order to find out, we're gonna count the number of pairwise disagreements between the two orders. That is, we're gonna take each possible pair of constructors (there are 45 pairs) and count the number of those where the order of the two teams has been reversed since last year. For instance, take Red Bull and McLaren: in 2023, Red Bull got more points than McLaren, but in 2024, McLaren ended up on top of Red Bull. That's one. On the other hand, Red Bull-Mercedes is not one of the pairs we're looking for: Red Bull is above Mercedes in both orders. So that's 2/45 pairs checked, only 43 more to go...

I'm not going to bore you with the details - the important thing is to count all pairs where the two teams' order is different in 2023 and 2024, but only once (that is, Ferrari-Williams and Williams-Ferrari are the same pair). In the end, I found the following pairs: McLaren-Red Bull, McLaren-Mercedes, McLaren-Ferrari, Ferrari-Mercedes, Ferrari-Red Bull, Haas-RB, Haas-Williams, Haas-Sauber, RB-Williams. That makes 9 (nine). This is the number value that describes the quality of my prediction.

Now, you can use this number directly as some sort of the-lower-the-better score, or you can take the remainder as a positive score (9 out of 45 pairs were wrong, so 36 was correct), but I personally like to normalize: 36/45=0.8=80%. I was 80% right. On a scale that ranges from the complete reversal of the actual order and predicting the order precisely, my prediction is at 4/5 of the way.

So there you have it. You can analyze this number, compare it to other's predictions, etc. If you're interested in evaluating the drivers' championship, it's a bit more complex because you have to handle drivers being replaced mid-season. (If you ask me, the easiest way is to ignore the new drivers, as you had no way of knowing they would come when you made your prediction.) Either way, this is the method to use.

The madness (theoretical background)

Let's talk about distances. While I'm sure you've used that word to mean "length of space between stuff" thousands of times in your life, in science, it actually has a broader, more abstract meaning: quantifiable difference. We use so-called distance metrics to measure how similar or different two things are.

In this more abstract meaning of the word "distance", we are not necessarily interested in questions like "How far is Sao Paolo from Las Vegas?" to which the answer is 9769 kilometres (or 6070 miles in American) but also "How far off are you if you say Max grabbed his title in Sao Paolo instead of Las Vegas?" to which the answer is one race. In the championship order example, we measured the so-called Kendall distance, which is specifically for rankings.

The beauty of measuring differences lies in a rule that is so obvious in the case of spatial distances that you wouldn't think twice about it: the triangle inequality. In case you don't remember from math class, the triangle inequality states that the sum of two sides of a triangle will always be longer than the third. In real life, it simply means that if you plan the shortest possible trip between two places and then decide to add a stop somewhere in between (not necessarily on the original route), your journey won't get any shorter. Duh.

However, when it comes to measuring differences, you have to be very careful to use a method that guarantees that the triangle inequality doesn't get violated. ...Well, to be honest, if you're only using it for evaluating predictions, the worst thing to happen is unfairness, but in other applications (where the distances are then used in further calculations), bigger issues can be caused. In fact, I was surprised how many scientists use a wrong metric for multidimensional vectors, which makes me a bit concerned... but it also makes me feel superior, so it's fine. (I'm joking, of course.)

Anyway, the triangle inequality problem is the reason why you can't just make up an easier method to score your predictions, even though it takes a long time to calculate the Kendall distance - if you want to evaluate your WDC predictions, you have to check 190(!) individual pairs of drivers. Simpler methods do not yield fair and reliable results.

Variations

I know what you're thinking: This method is way too simple! I want something more complex so that it is easier to mess up.

Joking aside, there are other aspects to consider when evaluating predictions. For example, you might want to take the points into account: if a driver only defeats another by a couple of points, switching them is a smaller mistake than switching two drivers with a bigger gap. If you want to include this in your evaluation, then instead of just counting the reversed pairs, you should be summing their points differences. Admittedly, this makes calculating positive scores and normalizing more complex, but it is still doable.

F1 is insistent on everyone getting different ranks: if two teams/drivers have the same amount of points, the number of wins is compared; if that is also the same, then the number of 2nd finishes; etc. However, there might be other sports or other rankings that aren't so strict, and two participants may have the same rank. Order distances can still be calculated: if a pair has the same rank in one of the orders but a different one in the other, the number of reversed pairs has to be increased by 0.5 - as in it's only half-reversed.

Sometimes, people predict only the order of the top drivers (e.g. the top 5) before a race. This can also be evaluated against the real top 5 by counting the reversed pairs of drivers that appear among the top 5 in at least one of the lists.

Let's say we're considering the Sainz-Norris pair, where Sainz has beaten Norris in the race, but both ended up in the top 5. If both drivers appear in the predicted top 5, then you can check if you guessed their order correctly as usual. If only Sainz is included in your top 5 and Norris isn't, that means you correctly predicted that Sainz would end up in a higher position than Norris. On the other hand, if you have Norris in your top 5 but not Sainz, it means you incorrectly expected Norris to perform better than Sainz, and you have to include the Sainz-Norris pair among your mistakes. The only tricky situation is where neither of them is in your "top 5" prediction. In this case, you can be optimistic and say you would have guessed their order correctly (or pessimistic and say you would have missed); but for me, the fairest solution seems to go neutral and add 0.5 to the number of reversed pairs.

Another idea is to consider the positions: you might say that it is more important to guess the top than the bottom correctly. For instance, switching the first and the second best drivers is a bigger mistake than switching the 15th and the 16th. Including this in the evaluation leads to very complicated calculations, but basically, weights have to be assigned to the positions (this part involves complicated logarithmic functions), and then, for each reverse pair, you multiply the two position weights and sum all those numbers.

These methods yield correct scores, so now you can go wild and compare predictions with all of your friends (that is, if you still have friends after spending so much time explaining the proper scoring system to them). Have fun!

P.S. I hope you've enjoyed this post, but even if you didn't, don't worry! I promise I won't post anything anywhere near as scientific as this one in the foreseeable future.

I have a couple of posts in progress, and they will be informative and fun. There will even be another post detailing my experience about an F1 (and Williams!) related adventure, which I can't wait to share with you, but first, I need to... you know... have it. See ya!

Rebus T. Farkas